Gerçel sayılar
Rasyonel sayılar Kümesi’nin standart metriğe göre bütünlenmesiyle elde edilen kümedir. Reel Sayılar Kümesi  sembolüyle gösterilir.
sembolüyle gösterilir.
Basit aritmetik teknikleriyle kolayca ispatlanabileceği üzere, tüm rasyonel sayıların tekrar eden birer ondalık açılımı vardır. Mesela
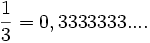
veya
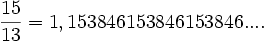
eşitliklerinde olduğu gibi. Burada dikkat edilmesi gereken, ondalık basamaklardaki rakamların bir süre sonra bloklar halinde periyodik tekrar etme özelliğidir. Rasyonel sayılardan reel sayıları elde etme işlemini ise rasyonel sayılara ondalık açılımındaki rakamların periyodik tekrar etmediği sayıların eklenmesi olarak düşünülebilir. Bu tür sonradan elde ettiğimiz reel sayılara irrasyonel sayılar denir.
İrrasyonel Sayılara Örnekler:

Bazı Yan Bilgiler:
- Tam kare olmayan hiç bir doğal sayının karekökü rasyonel değildir.
- Rasyonel Sayılar Kümesi’nin sayılabilir olmasına karşılık Reel Sayılar Kümesi sayılamazdır.
- İrrasyonel sayılar da kendi içlerinde "cebirsel sayılar" ve "aşkın sayılar" olarak ikiye ayrılırlar.
- İrrasyonel sayıların varlığının ilk Yunan matematikçi Pisagor tarafından anlaşılmış olduğu görüşü yaygındır. Fakat Pisagor bu sayıların evrenin düzenine aykırı olduğunu düşünmüş ve öğrencilerine bu sayıların varlığını açıklamayı yasaklamıştır.
- Arşimet Özelliği: x ve y birer reel sayı olsun ve x sıfırdan büyük olsun. Bu durumda
- nx > y özelliğini sağlayan bir n doğal sayısı vardır.